|
|||||||||||
|
Purpose: Detect Non-Randomness |
The runs test (Bradley, 1968) can be used to decide if a data set is from a random process. A run is defined as a series of increasing values or a series of decreasing values. The number of increasing, or decreasing, values is the length of the run. In a random data set, the probability that the (I+1)th value is larger or smaller than the Ith value follows a binomial distribution, which forms the basis of the runs test. | ||||||||||
| Typical Analysis and Test Statistics |
The first step in the runs test is to count the number of runs
in the data sequence. There are several ways to define runs
in the literature, however, in all cases the formulation must
produce a dichotomous sequence of values. For example, a
series of 20 coin tosses might produce the following sequence
of heads (H) and tails (T).
| ||||||||||
| Definition |
We will code values above the median as positive and values
below the median as negative. A run is defined as a series
of consecutive positive (or negative) values.
The runs test is defined as:
|
||||||||||
|
Runs Test Example |
A runs test was performed for 200 measurements of beam deflection
contained in the LEW.DAT data set.
H0: the sequence was produced in a random manner Ha: the sequence was not produced in a random manner Test statistic: Z = 2.6938 Significance level: α = 0.05 Critical value (upper tail): Z1-α/2 = 1.96 Critical region: Reject H0 if |Z| > 1.96Since the test statistic is greater than the critical value, we conclude that the data are not random at the 0.05 significance level. |
||||||||||
| Question |
The runs test can be used to answer the following question:
|
||||||||||
| Importance |
Randomness is one of the key
assumptions in determining
if a univariate statistical process is in control. If
the assumptions of constant location and scale, randomness,
and fixed distribution are reasonable, then the univariate
process can be modeled as:
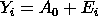 |
||||||||||
| Related Techniques |
Autocorrelation Run Sequence Plot Lag Plot |
||||||||||
| Case Study | Heat flow meter data | ||||||||||
| Software | Most general purpose statistical software programs support a runs test. Both Dataplot code and R code can be used to generate the analyses in this section. | ||||||||||
Gertrude Cox : Gertrude Mary Cox (of Experimental Statistics at North Carolina State University. She was later appointed director of both the Institute of Statistics of 1900 - 1978) was an influential American statistician and founder of the department the Consolidated University of North Carolina and the Statistics Research Division of North Carolina State University. Her most important and influential research dealt with experimental design; she wrote an important book on the subject with W. G. Cochran. In 1949 Cox became the first female elected into the International Statistical Institute and in 1956 she was president of the American Statistical Association. From 1931 to 1933 Cox undertook graduate studies in statistics at the University of California at Berkeley , then returned to Iowa State College as assistant in the Statistical Laboratory. Here she worked on the design of experiments . In 1939 she was appointed assistant professor of statisti...
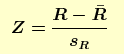
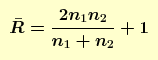
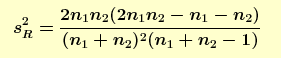
Comments
Post a Comment