Skip to main content

Chi square distribution

Chi-Square Distribution

Probability Density FunctionThe chi-square distribution results when nu independent variables with standard normal distributions are squared and summed. The formula for the probability density function of the chi-square distribution isf(x) = EXP(-x/2)*x**(nu/2 - 1)/(2**(nu/2)*GAMMA(nu/2)) x >= 0
where nu is the shape parameter and GAMMA is the gamma function. The formula for the gamma function is
GAMMA(a) = INTEGRAL[t**(a-1)*EXP(-t)dt] where the integration is from 0 to infinity
In a testing context, the chi-square distribution is treated as a "standardized distribution" (i.e., no location or scale parameters). However, in a distributional modeling context (as with other probability distributions), the chi-square distribution itself can be transformed with a location parameter, 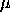mu, and a scale parameter, sigma.
The following is the plot of the chi-square probability density function for 4 different values of the shape parameter.
plot of the chi-square probability density function for 4 different values of the shape parameter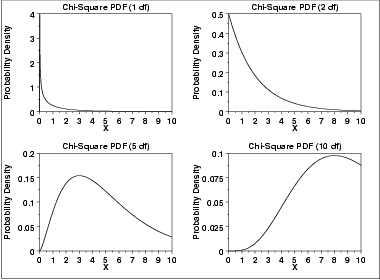
Cumulative Distribution FunctionThe formula for the cumulative distribution function of the chi-square distribution isF(x) = gamma(nu/2,x/2)/GAMMA(nu/2) for x >= 0
where GAMMA is the gamma function defined above and gamma is the incomplete gamma function. The formula for the incomplete gamma function is
GAMMA(a,x) = INTEGRAL[t**(a-1)*EXP(-t)dt] where the integration is from 0 to x
The following is the plot of the chi-square cumulative distribution function with the same values of  as the pdf plots above.
plot of the chi-square cumulative distribution function with the same values of nu as the pdf plots above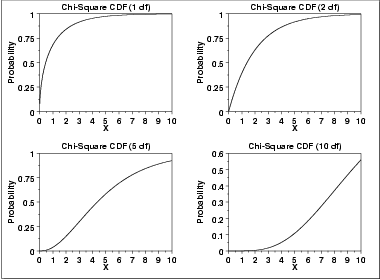
Percent Point FunctionThe formula for the percent point function of the chi-square distribution does not exist in a simple closed form. It is computed numerically.The following is the plot of the chi-square percent point function with the same values of nu as the pdf plots above.
plot of the chi-square percent point function with the same values of nu as the pdf plots above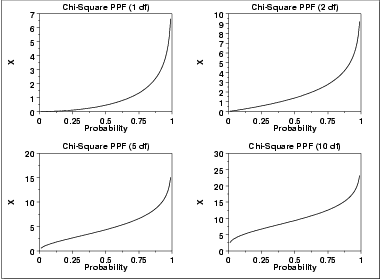
Other Probability FunctionsSince the chi-square distribution is typically used to develop hypothesis tests and confidence intervals and rarely for modeling applications, we omit the formulas and plots for the hazard, cumulative hazard, survival, and inverse survival probability functions.
Common Statistics
Meannu
Medianapproximately nu - 2/3 for large nu
Modenu -2 for nu > 2
Range0 to positive infinity
Standard DeviationSQRT(2*nu)
Coefficient of VariationSQRT(2/nu)
Skewness2**1.5/SQRT(nu)
Kurtosis3 + 12/nu
Parameter EstimationSince the chi-square distribution is typically used to develop hypothesis tests and confidence intervals and rarely for modeling applications, we omit any discussion of parameter estimation.
CommentsThe chi-square distribution is used in many cases for the critical regions for hypothesis tests and in determining confidence intervals. Two common examples are the chi-square test for independence in an RxC contingency table and the chi-square test to determine if the standard deviation of a population is equal to a pre-specified value.
SoftwareMost general purpose statistical software programs support at least some of the probability functions for the chi-square distribution.

Comments

Post a Comment

Popular posts from this blog

Lognormal distribution

Lognormal Distribution Probability Density Function A variable X is lognormally distributed if Y = LN(X) is normally distributed with "LN" denoting the natural logarithm. The general formula for the  probability density function  of the lognormal distribution is where   is the  shape parameter ,   is the  location parameter  and  m is the  scale parameter . The case where   = 0 and  m  = 1 is called the  standard lognormal distribution . The case where   equals zero is called the 2-parameter lognormal distribution. The equation for the standard lognormal distribution is Since the general form of probability functions can be  expressed in terms of the standard distribution , all subsequent formulas in this section are given for the standard form of the function. The following is the plot of the lognormal probability density function for four values of  . There are several commo...
Post a Comment
Read more

Runs Test for Detecting Non-randomness

Runs Test for Detecting Non-randomness Purpose: Detect Non-Randomness The runs test ( Bradley, 1968 ) can be used to decide if a data set is from a random process. A run is defined as a series of increasing values or a series of decreasing values. The number of increasing, or decreasing, values is the length of the run. In a random data set, the probability that the ( I +1)th value is larger or smaller than the I th value follows a binomial distribution , which forms the basis of the runs test. Typical Analysis and Test Statistics The first step in the runs test is to count the number of runs in the data sequence. There are several ways to define runs in the literature, however, in all cases the formulation must produce a dichotomous sequence of values. For example, a series of 20 coin tosses might produce the f...
Post a Comment
Read more

Poisson distribution

Poisson Distribution Probability Mass Function The Poisson distribution is used to model the number of events occurring within a given time interval.The formula for the Poisson probability mass function is  is the shape parameter which indicates the average number of events in the given time interval. The following is the plot of the Poisson probability density function for four values of  . Cumulative Distribution Function The formula for the Poisson cumulative probability function is The following is the plot of the Poisson cumulative distribution function with the same values of   as the pdf plots above. Percent Point Function The Poisson percent point function does not exist in simple closed form. It is computed numerically. Note that because this is a discrete distribution that is only defined for integer values of  x , the percent point function is not smooth in the way the percent point function typically is for a continuous distribution....
Post a Comment
Read more