Mann-Whitney U Test
{From the Institute of Phonetic Sciences (IFA): http://www.fon.hum.uva.nl/}
The Mann-Whitney U test is used to analyze rank-ordered data. This test is a nonparametric alternative to the independent-sample, Student t test, and yields results identical to those obtained from the Wilcoxon Two Independent Samples Test.
H0: The populations from which the two samples are taken have identical median values. To be complete, the two populations have identical distributions.
Assumptions:
None that matter.
Scale:
Ordinal.
Procedure:
Rank the combined set of data from the two groups from lowest to highest with tied scores receiving a rank equal to the average position of those scores in the ordered array (see the example). Compute
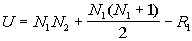
For this example N1 = 9, and N2 = 11. The sum of the ranks (R1) is 139. Substituting these values into the equation given above yields:
If you have already computed U and want to determine its level of significance, click here: HERE
{From the Institute of Phonetic Sciences (IFA): http://www.fon.hum.uva.nl/}
The Mann-Whitney U test is used to analyze rank-ordered data. This test is a nonparametric alternative to the independent-sample, Student t test, and yields results identical to those obtained from the Wilcoxon Two Independent Samples Test.
H0: The populations from which the two samples are taken have identical median values. To be complete, the two populations have identical distributions.
Assumptions:
None that matter.
Scale:
Ordinal.
Procedure:
Rank the combined set of data from the two groups from lowest to highest with tied scores receiving a rank equal to the average position of those scores in the ordered array (see the example). Compute
where U is the Mann-Whitney statistic, N1
and N2 are the number of cases in samples 1 and 2,
respectively, and R1 is the sum of the ranks for the first
sample.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
For this example N1 = 9, and N2 = 11. The sum of the ranks (R1) is 139. Substituting these values into the equation given above yields:
We can compare this value to the Critical Values given in Tables of Critical Values for the Mann-Whitney U Test, where we learn that the probability of a U of 5, under the null hypothesis, when N1 = 9, and N2 = 11 is less than .01. We conclude that the groups are significantly different.U = (9 x 11) + [ 9(9 + 1) / 2 ] - 139
= 99 + (9)(10)/2 -139
= 99 + 45 - 139
= 5
If you have already computed U and want to determine its level of significance, click here: HERE
Comments
Post a Comment