| |||||||||||||
| Probability Density Function | The F distribution is the ratio of two chi-square distributions with degrees of freedom  and and  , respectively, where each chi-square has first been divided by its degrees of freedom. The formula for the probability density function of the F distribution is , respectively, where each chi-square has first been divided by its degrees of freedom. The formula for the probability density function of the F distribution is![[GAMMA((nu1+nu2)/2)*(nu1/nu2)**(nu1/2)*x**((nu2/2)-1)]/
GAMMA(nu1/2)*GAMMA(nu2/2)*(1 + Nu1*x/Nu2)**((nu1+nu2)/2)]](http://www.itl.nist.gov/div898/handbook/eda/section3/eqns/fpdf.gif)  and and  are the shape parameters and are the shape parameters and  is the gamma function. The formula for the gamma function is is the gamma function. The formula for the gamma function is![GAMMA(a) = INTEGRAL[t**(a-1)*EXP(-t)dt] where the
integration is from 0 to infinity](http://www.itl.nist.gov/div898/handbook/eda/section3/eqns/gammfunc.gif) 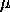 , and a scale parameter, , and a scale parameter, 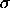 .The following is the plot of the F probability density function for 4 different values of the shape parameters. .The following is the plot of the F probability density function for 4 different values of the shape parameters. | ||||||||||||
| Cumulative Distribution Function | The formula for the Cumulative distribution function of the F distribution is  / ( / ( + +  *x) and Ik is the incomplete beta function. The formula for the incomplete beta function is *x) and Ik is the incomplete beta function. The formula for the incomplete beta function is![I(k)(x,alpha,beta) = INTEGRAL[t**(alpha-1)*(1-t)**(beta-1)dt]/
B(alpha,beta) where the integration is from 0 to x](http://www.itl.nist.gov/div898/handbook/eda/section3/eqns/ibetfunc.gif)   and and  as the pdf plots above. as the pdf plots above. | ||||||||||||
| Percent Point Function | The formula for the percent point function of the F distribution does not exist in a simple closed form. It is computed numerically.The following is the plot of the F percent point function with the same values of  and and  as the pdf plots above. as the pdf plots above.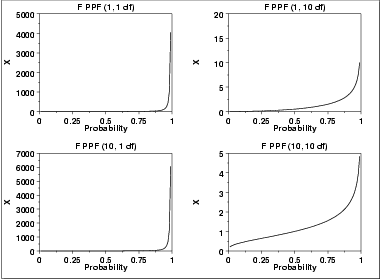 | ||||||||||||
| Other Probability Functions | Since the F distribution is typically used to develop hypothesis tests and confidence intervals and rarely for modeling applications, we omit the formulas and plots for the hazard, cumulative hazard, survival, and inverse survival probability functions. | ||||||||||||
| Common Statistics | The formulas below are for the case where the location parameter is zero and the scale parameter is one.
| ||||||||||||
| Parameter Estimation | Since the F distribution is typically used to develop hypothesis tests and confidence intervals and rarely for modeling applications, we omit any discussion of parameter estimation. | ||||||||||||
| Comments | The F distribution is used in many cases for the critical regions for hypothesis tests and in determining confidence intervals. Two common examples are the analysis of variance and the F test to determine if the variances of two populations are equal. | ||||||||||||
| Software | Most general purpose statistical software programs support at least some of the probability functions for the F distribution | ||||||||||||
Runs Test for Detecting Non-randomness Purpose: Detect Non-Randomness The runs test ( Bradley, 1968 ) can be used to decide if a data set is from a random process. A run is defined as a series of increasing values or a series of decreasing values. The number of increasing, or decreasing, values is the length of the run. In a random data set, the probability that the ( I +1)th value is larger or smaller than the I th value follows a binomial distribution , which forms the basis of the runs test. Typical Analysis and Test Statistics The first step in the runs test is to count the number of runs in the data sequence. There are several ways to define runs in the literature, however, in all cases the formulation must produce a dichotomous sequence of values. For example, a series of 20 coin tosses might produce the f...





Comments
Post a Comment