Skip to main content

Lognormal distribution

Lognormal Distribution

Probability Density FunctionA variable X is lognormally distributed if Y = LN(X) is normally distributed with "LN" denoting the natural logarithm. The general formula for the probability density function of the lognormal distribution is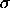f(x) = EXP(-((ln((x-theta)/m))**2/(2*sigma*2))/ ((x-theta)*sigma*SQRT(2*PI)) x >= theta; sigma, m > 0
where sigma is the shape parameter, theta is the location parameter and mis the scale parameter. The case where  = 0 and m = 1 is called the standard lognormal distribution. The case where theta equals zero is called the 2-parameter lognormal distribution.
The equation for the standard lognormal distribution is
f(x) = EXP(-(log(x)**2/(2*sigma**2))/(x*sigma*SQRT(2*PI)) x >= 0; sigma > 0
Since the general form of probability functions can be expressed in terms of the standard distribution, all subsequent formulas in this section are given for the standard form of the function.
The following is the plot of the lognormal probability density function for four values of sigma.
plot of the lognormal probability density function for four values of sigma
There are several common parameterizations of the lognormal distribution. The form given here is from Evans, Hastings, and Peacock.
Cumulative Distribution FunctionThe formula for the cumulative distribution function of the lognormal distribution isF(x) = PHI(LN(x)/sigma) x >= 0; sigma > 0
where PHI is the cumulative distribution function of the normal distribution.
The following is the plot of the lognormal cumulative distribution function with the same values of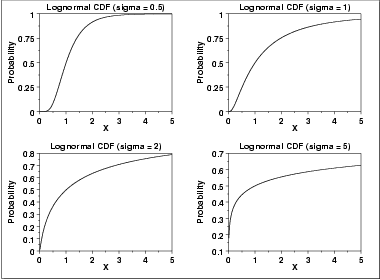 sigma as the pdf plots above.
plot of the lognormal cumulative distribution function
Percent Point FunctionThe formula for the percent point function of the lognormal distribution isG(p) = EXP(sigma*PHI**(-1)(p)) 0 <= p < 1; sigma > 0
where PHI**(-1) is the percent point function of the normal distribution.
The following is the plot of the lognormal percent point function with the same values of 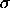sigma as the pdf plots above.
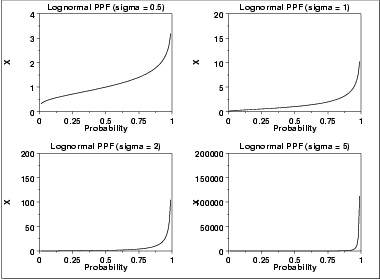plot of the lognormal percent point function
Hazard FunctionThe formula for the hazard function of the lognormal distribution is(1/(sigma*x))*phi(LOG(x)/sigma)/PHI(-LOG(x)/sigma) x > 0; sigma > 0
where phi is the probability density function of the normal distributionand PHI is the cumulative distribution function of the normal distribution.
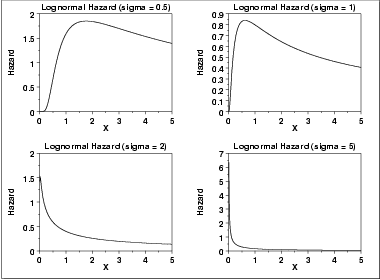The following is the plot of the lognormal hazard function with the same values of  as the pdf plots above.
plot of the lognormal hazard function
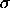Cumulative Hazard FunctionThe formula for the cumulative hazard function of the lognormal distribution isH(x) = -LN(1 - PHI(LN(x)/sigma)) x >= 0; sigma > 0
where PHI is the cumulative distribution function of the normal distribution.
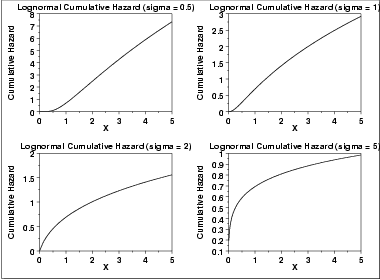The following is the plot of the lognormal cumulative hazard function with the same values of sigma as the pdf plots above.
plot of the lognormal cumulative hazard function
Survival FunctionThe formula for the survival function of the lognormal distribution isS(x) = 1 - PHI(LN(x)/sigma) x >= 0; sigma > 0
where PHI is the cumulative distribution function of the normal distribution.
The following is the plot of the lognormal survival function with the same values of 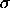sigma as the pdf plots above.
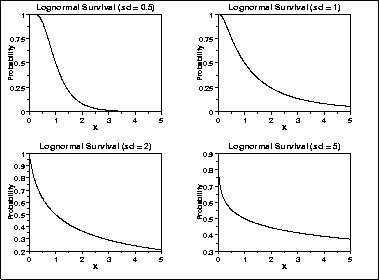plot of the lognormal survival function
Inverse Survival FunctionThe formula for the inverse survival function of the lognormal distribution isZ(p) = EXP(sigma*PHI**(-1)(1-p)) 0 <= p < 1; sigma > 0
where PHI**(-1) is the percent point function of the normal distribution.
The following is the plot of the lognormal inverse survival function with the same values of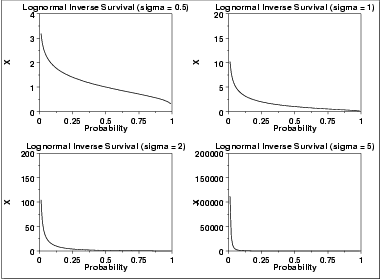 sigma as the pdf plots above.
plot of the lognormal inverse survival function
Common StatisticsThe formulas below are with the location parameter equal to zero and the scale parameter equal to one.
MeanEXP(0.5*sigma**2
MedianScale parameter m (= 1 if scale parameter not specified).
Mode1/EXP(sigma**2)
RangeZero to positive infinity
Standard DeviationSQRT(EXP(sigma**2)*(EXP(sigma**2)-1))
Skewness(EXP(sigma**2)+2)**SQRT(EXP(sigma**2)-1))
KurtosisEXP(sigma**2)**4+2*EXP(sigma**2)**3+3*EXP(sigma**2)**2-3
Coefficient of VariationSQRT(EXP(sigma**2) - 1)
Parameter EstimationThe maximum likelihood estimates for the scale parameter, m, and the shape parameter, 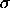sigma, are
    mhat = EXP(uhat)
and
    sigmahat = SQRT{SUM[i=1 to N][(LOG(X(i))-mu)**2]/N}
where
    Uhat = SUM[i=1 to N][LOG(X(i))]/N
If the location parameter is known, it can be subtracted from the original data points before computing the maximum likelihood estimates of the shape and scale parameters.
CommentsThe lognormal distribution is used extensively in reliabilityapplications to model failure times. The lognormal and Weibulldistributions are probably the most commonly used distributions in reliability applications.
SoftwareMost general purpose statistical software programs support at least some of the probability functions for the lognormal distribution.

Comments

Post a Comment

Popular posts from this blog

The most femiliar statisticians

Gertrude Cox :   Gertrude Mary Cox (of Experimental Statistics at North Carolina State University. She was later appointed director of both the Institute of Statistics of 1900 - 1978) was an influential American statistician and founder of the department the Consolidated University of North Carolina and the Statistics Research Division of North Carolina State University. Her most important and influential research dealt with experimental design; she wrote an important book on the subject with W. G. Cochran. In 1949 Cox became the first female elected into the International Statistical Institute and in 1956 she was president of the American Statistical Association. From 1931 to 1933 Cox undertook graduate studies in statistics at the  University of California at Berkeley , then returned to Iowa State College as assistant in the Statistical Laboratory. Here she worked on the  design of experiments . In 1939 she was appointed assistant professor of statisti...
Post a Comment
Read more

Runs Test for Detecting Non-randomness

Runs Test for Detecting Non-randomness Purpose: Detect Non-Randomness The runs test ( Bradley, 1968 ) can be used to decide if a data set is from a random process. A run is defined as a series of increasing values or a series of decreasing values. The number of increasing, or decreasing, values is the length of the run. In a random data set, the probability that the ( I +1)th value is larger or smaller than the I th value follows a binomial distribution , which forms the basis of the runs test. Typical Analysis and Test Statistics The first step in the runs test is to count the number of runs in the data sequence. There are several ways to define runs in the literature, however, in all cases the formulation must produce a dichotomous sequence of values. For example, a series of 20 coin tosses might produce the f...
Post a Comment
Read more