Correlation Methods
- This method requires multiple numeric data columns whose values should be stored in a single worksheet.
- The theoretical sampling distribution of the correlation coefficient can be approximated by the normal distribution when the value of a population correlation ρ = 0, but as the value of r deviates from zero, the sampling distribution becomes increasingly skewed. Fisher's ztransformation transforms a skewed sampling distribution into a normalized format.
![\rho_{X,Y}={\mathrm{cov}(X,Y) \over \sigma_X \sigma_Y} ={E[(X-\mu_X)(Y-\mu_Y)] \over \sigma_X\sigma_Y}](https://upload.wikimedia.org/math/c/6/8/c684841ca41265c95ea22bc23c1e2031.png)
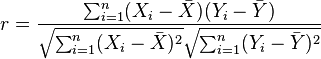
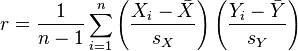

![E[(X-E(X))(Y-E(Y))]=E(XY)-E(X)E(Y),\,](https://upload.wikimedia.org/math/d/6/8/d68b84931c79ab42b6a9374ffd5a4179.png)

Spearman's rank correlation coefficient
In applications where duplicate values (ties) are known to be absent, a simpler procedure can be used to calculate ρ.[3][4]Differences between the ranks of each observation on the two variables are calculated, and ρ is given by:Note that this latter method should not be used in cases where the data set is truncated; that is, when the Spearman correlation coefficient is desired for the top X records (whether by pre-change rank or post-change rank, or both), the user should use the Pearson correlation coefficient formula given above.
between the ranks of each observation on the two variables are calculated, and ρ is given by:Note that this latter method should not be used in cases where the data set is truncated; that is, when the Spearman correlation coefficient is desired for the top X records (whether by pre-change rank or post-change rank, or both), the user should use the Pearson correlation coefficient formula given above.- Sort the data by the first column (
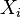 ). Create a new column
). Create a new column 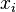 and assign it the ranked values 1,2,3,...n.
and assign it the ranked values 1,2,3,...n. - Next, sort the data by the second column (
 ). Create a fourth column
). Create a fourth column  and similarly assign it the ranked values 1,2,3,...n.
and similarly assign it the ranked values 1,2,3,...n. - Create a fifth column
 to hold the differences between the two rank columns (
to hold the differences between the two rank columns (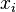 and
and  ).
). - Create one final column
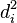 to hold the value of column
to hold the value of column  squared.
squared. 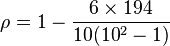
Correlation and Covariance Matrices
You can generate a correlation or covariance matrix from numeric data columns, and have the choice of storing the computation results in an-autogenerated worksheet, or display the results in a table format whose values can be color coded.
An example of a correlation matrix displayed as a color-coded table is shown below.

Using Fisher's z Transformation (zr)
This option is provided to allow transforming a skewed sampling distribution into a normalized format.
The relationship between Pearson's product-moment correlation coefficient and the Fisher-Transformed values are shown in the right-hand side image.
The image below shows the Fisher-transformed values of the correlation matrix displayed above.
|  |

Pearson Product-Moment Correlation Coefficient (Pearson's r)
For a sample[edit]
Pearson's correlation coefficient when applied to a sample is commonly represented by the letter r and may be referred to as the sample correlation coefficient or the sample Pearson correlation coefficient. We can obtain a formula for r by substituting estimates of the covariances and variances based on a sample into the formula above. That formula for r is:
An equivalent expression gives the correlation coefficient as the mean of the products of the standard scores. Based on a sample of paired data (Xi, Yi), the sample Pearson correlation coefficient is
where
Mathematical properties[edit]
The absolute value of both the sample and population Pearson correlation coefficients are less than or equal to 1. Correlations equal to 1 or -1 correspond to data points lying exactly on a line (in the case of the sample correlation), or to a bivariate distribution entirely supported on a line (in the case of the population correlation). The Pearson correlation coefficient is symmetric: corr(X,Y) = corr(Y,X).
A key mathematical property of the Pearson correlation coefficient is that it is invariant (up to a sign) to separate changes in location and scale in the two variables. That is, we may transform X to a + bX and transform Y to c + dY, where a, b, c, and d are constants, without changing the correlation coefficient (this fact holds for both the population and sample Pearson correlation coefficients). Note that more general linear transformations do change the correlation: see a later section for an application of this.
The Pearson correlation can be expressed in terms of uncentered moments. Since μX = E(X), σX2 = E[(X − E(X))2] = E(X2) − E2(X) and likewise for Y, and since
the correlation can also be written as
Example [edit]
In this example, we will use the raw data in the table below to calculate the correlation between the IQ of a person with the number of hours spent in front of TV per week.
IQ, 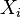 | Hours of TV per week,  |
| 106 | 7 |
| 86 | 0 |
| 100 | 27 |
| 101 | 50 |
| 99 | 28 |
| 103 | 29 |
| 97 | 20 |
| 113 | 12 |
| 112 | 6 |
| 110 | 17 |
First, we must find the value of the term 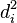 . To do so we use the following steps, reflected in the table below.
. To do so we use the following steps, reflected in the table below.
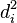 . To do so we use the following steps, reflected in the table below.
. To do so we use the following steps, reflected in the table below.IQ, 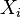 | Hours of TV per week,  | rank 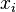 | rank  |  | 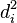 |
| 86 | 0 | 1 | 1 | 0 | 0 |
| 97 | 20 | 2 | 6 | −4 | 16 |
| 99 | 28 | 3 | 8 | −5 | 25 |
| 100 | 27 | 4 | 7 | −3 | 9 |
| 101 | 50 | 5 | 10 | −5 | 25 |
| 103 | 29 | 6 | 9 | −3 | 9 |
| 106 | 7 | 7 | 3 | 4 | 16 |
| 110 | 17 | 8 | 5 | 3 | 9 |
| 112 | 6 | 9 | 2 | 7 | 49 |
| 113 | 12 | 10 | 4 | 6 | 36 |
With 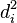 found, we can add them to find
found, we can add them to find  . The value of n is 10. So these values can now be substituted back into the equation,
. The value of n is 10. So these values can now be substituted back into the equation,
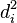 found, we can add them to find
found, we can add them to find  . The value of n is 10. So these values can now be substituted back into the equation,
. The value of n is 10. So these values can now be substituted back into the equation,
which evaluates to ρ = -29/165 = −0.175757575... with a P-value = 0.6864058 (using the t distribution)
This low value shows that the correlation between IQ and hours spent watching TV is very low.

nice krish.....
ReplyDeleteThank u Mano.....
Delete